September 21, 2010. Limits, Continuity, and Derivatives Oh My!

We started class with a warm up, which was really just more practice with continuity. It really reinforced the two things we need to remember: what makes a function continuous or discontinuous. To recap, the three rules of continuity are: f(x) is continuous at point c if:

1) f(c) exists (not a hole or an asymptote, volcanic or otherwise)

2) limit of f(x) approaches c exists (no breaks or normal asymptotes)

3) the above limit is equal to f(c)

A function is continuous if it is continuous along all points within its domain.

Also, remember the two types of discontinuity:

1) A removable discontinuity is a single point, either a hole or a single discontinuous value (in a piecewise defined function it would be a clause that said f(x) = 6 if x=6.)

2) A non-removable discontinuity is a jump, or break in an otherwise continuous graph

(see graph below)

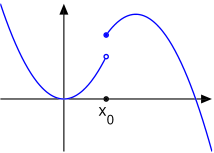
This WILL be on the test Thursday, so study up.

After finishing with the warm up, we went over the quiz, which seemed to go reasonably smoothly for everyone. The only issues that came up were addressed quickly, though discontinuities did come up at least once.

From the quiz we jumped right into assignment 7 (remember that one, two posts down?). Specifically, we demonstrated how you could use different methods to solve the problems from 5, most importantly part c (with natural log of x in the numerator). We also covered number 8, and went over several methods to solve it. For average rate of change, we can just graph it, and draw a line between the two points. The slope of this line (called a secant line) is equal to the rate of change between those two points.

For the instantaneous rate of change, it gets kinda tricky. Firstly, knowing that instantaneous rate of change is also the derivative, we can use nDeriv on our calculators (nDeriv lives under the Math key, option #8). Secondly, we can plug it into wolframalpha and get a perfect answer. Finally, we can take

Using c as whatever point you are trying to find the instantaneous rate of change at, then solving the limit as we have been doing for ages now. This is a big idea, but WILL NOT be on the test Thursday.

Mr. O'Brien then handed out the next assignment (down below). It looks like a practice test (which it basically is) but it will be collected on friday along with #5,6,7. Use it however you like, but it might be a really big help on thursday's test.

Thursday's test will cover Limits and Continuity.

For study help we return to ucdavis, as well as voyaging into the realm of the complicated with Paul . Remember: Test Thursday, Study hard!