September 13, 2010 Scribe Post

We began class today by performing a warm up exercise concerning the indeterminate form. First we were to find f(x) and g(x) such that f(c)=g(c)=0 and is:
1.
a) 0
b) 17
c)
d) D.N.E.

In other words, you are looking for an indeterminate case where you get zero in the numerator and zero in the denominator, such that it has the following properties: the limit is 0 or 17 or or D.N.E., and the functions values are each zero when we evaluate at this thing that we are approaching. This is other wise known as the indeterminate form.

Then we were to attempt to find the following equations without technology:
2.
a)
b)
c)

Before the class revealed their answers, Mr. O'Brien commented on a key idea which is that a function doesn't have a limit in general, it has a limit at a point. So you are never going to just a and a function, you going to have x approaching something otherwise you cannot possibly have a value for the limit.

Next, in order to test our answers we checked to make sure we had a fraction limit and also that both the numerator and the denominator were zeros. And in order to find the limit values, we used a table to evaluate our functions.

By looking at the table we declared that an answer to a) for the first question is . This function has a limit which is approaching zero. This is because as x gets very close to zero, the y value gets closer and closer to zero as well.


Next, in order to find an answer to b) for the first question, we decided to look at the problem algebraically. We created the function which when evaluated equals 17. We then multiplied this by the fufoo (funny form of one) and it gave us . Both of the functions and are identical at all values except for 3 (because the fufoo caused a hole at 3). Mr. O'Brien also comments that there are an infinite amount of answers to this problem but the key is using the fufoo.

In order to find where the limit D.N.E., instead of creating a hole, we need to create a gap, a break, or a non removable discontinuity. And in order to get that we need to include absolute value on the numerator so the equation looks like this: . This means that as we approach zero from the left and the right we are not getting one value but two which means that the limit does not exist. In order to better visualize this I replicated the graph:

Overall for all three problems Mr. O'Brien emphasized that if you have any function you can add a hole to it and it does not change the limit value.

Lastly for c) we got . We had instead of because, when you reduce you get which gives you a volcano asymptote. This means that you will have an infinite value for y when you approach 0.


Next we evaluated the infinite limits for question 2 without a calculator. The first one is a natural log function which means the domain is everything above zero, there is no y intercept, and the x intercept is 1. Now to evaluate we look at t as it approaches infinity which is zero. This means that we are considering the natural log of zero which is negative infinity. Because as x approaches zero it has a vertical asymptote. So if you know the parent function you can reason through the limit without the technology.

Now for b) and c) of question 2 it helps to think about how fast the fractions are growing. For b) the limit is approaching zero because the numerator is approaching infinity slower than the denominator. For c) the numerator is growing so much faster than the denominator making the limit be infinity.

Next we evaluated the quiz. An important not was that for number 4 you need to include the actual value which is opposed to 1.732 which is an approximate value. In addition, Mr. O'Brien noted that by the end of class, the entire first side of the quiz should be able to be done without a calculator. For number 7 Mr. O'Brien noted that students need to provide an explanation or a counter example.
Next we "NAG" (to take a look at the numeric, algebric, graphic) the function . We determined that the limit was 1 and there was a gap at (0,1). The graph looked like this:

Mr. O'Brien then adds that you cannot see the hole, but you know that there is a hole because the function is not defined at zero. Next we looked at this algebraically because this one limit is the foundation of all of the calculus of trigonometry that we are going to do. We noticed that as x gets bigger and bigger the end behavior get smaller and smaller giving you a horizontal asymptote of zero. This is because the denominator gets bigger and bigger and the numerator is oscillating between 1 and negative 1.


We now turned our attention to The Squeeze Theorem (aka The Sandwich Theorem) which states: If on some open interval containing c and then .

We then reviewed an example of this which is and looks like this:

This has to do with the squeeze theorem because. This concept is better viewed in the graph:
Here we can see a visual of the squeeze therom. We know that the limit of both and is zero meaning that the limit of is zero as well.

Next in order to look at as a sandwich equation we looked at the following diagram:

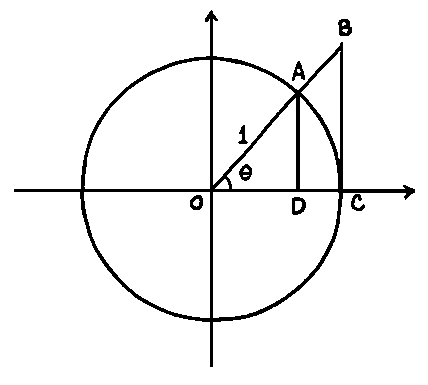
In the diagram: AD= and BC=
Now by using and we were able to come up with the following equation:

then multiplied by 2 and got:
then we divided by and got:
Lastly, we reciprocated the following equation and got:

Now since and we have applied the sandwich theorem for .

An additional diagram that might be helpful is the one Lange used in her blog:

In the last two minutes of class we were not able to complete two example problems which would help further our understanding of this theorem. So, it would be helpful to review example 3 and 4 on page 87-88 tonight before the homework. In addition, the following website http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/squeezedirectory/SqueezePrinciple.html provides numerous examples of the Squeeze theorem which will help as well.