Wednesday, December 15, 2010
Friday, December 10, 2010
Thursday, December 9, 2010
Wednesday, December 8, 2010
Friday, December 3, 2010
Thursday, December 2, 2010
Wednesday, December 1, 2010
Scribe Post Wednesday November 30th
Today was a pretty easy class overall. We started with looking at our quiz. We have a quiz tomorrow and there will be some of the same types of problems that were on this last quiz in the next one. There will still be questions on related rates, increasing and decreasing with respect to concavity, and Newton's Method. Essentially some form of questions 1, 2, and 3 will appear on the next quiz. After looking at the quiz we played the leap frog game. If you weren't here you can find the rules of the game on the blog below this post. We played this game for the majority of class and it was mainly to nail down some of the basic rules of concavity with respect to a function, its derivative and second derivative. An example for Annie is Where f''' is positive, f_________. The answer would be "is concave up". For some of the more difficult ones to understand Mr. O'Brien showed them up on the board and it seemed that many of them could be understood and solved if you drew out what the problem was asking. We used the last 15 minutes of class to do a problem from the 1999 AP test FRQ section (which can be found on this site http://www.etsu.edu/coe/uschool/facstaff/wells/AP%20Free%20Response/AB/1999.pdf. )
We did #4 in class and we were supposed to do #6 for homework as well as the rest of the homework that was on the iCal.
For more help with concavity http://archives.math.utk.edu/visual.calculus/3/graphing.6/index.html
Remember quiz tomorrow that will have questions like #1, 2, and 3
We did #4 in class and we were supposed to do #6 for homework as well as the rest of the homework that was on the iCal.
For more help with concavity http://archives.math.utk.edu/visual.calculus/3/graphing.6/index.html
Remember quiz tomorrow that will have questions like #1, 2, and 3
Tuesday, November 30, 2010
Leap Frog Game
Leap Frog Game
- Have students arrange their game cards on their desks
- After the first part of a statement is read using the Power Point presentation, students complete the statement by holding up the most complete correct answer
- Students who answer incorrectly must remain in their seats
- Students who answer correctly will proceed to the next available seat, “leap frogging” over the students who were incorrect
- Play continues until a student returns to his/her original seat
Rules:
- All functions are continuous and twice differentiable.
- Once a student holds up a card, they have committed and cannot change cards
Relationships Game—Part One (Basic Relationships)
- Uses the verbal cards (with “changes signs”)
- Bonus questions have two correct answers and allow the students to leap frog two desks. A student must hold up both correct cards to be eligible to leap.
Relationships Game—Part Two (Graphical and Numerical)
- Uses the numerical cards
- The functions represented by numerical tables are monotonic between data points
- Game card values represent x values
- Students hold up two cards to represent an interval
Relationships Game—Part Three (Linear Motion)
- Uses the verbal cards (with “equals zero”)
Sunday, November 28, 2010
Monday, November 22, 2010
Friday, November 19, 2010
Related Rates Warm up
Mr. O'Brien graduated from Camden-Rockport High School in 1990. How would you do on his AP Calculus exam? Let's try Question 4!
Thursday, November 18, 2010
Wednesday, November 17, 2010
Monday, November 15, 2010
Scribe 11/15
Today we started class by looking at Sophie's blog post about Newton's Method, and discussed how using spreadsheets can be very helpful in speeding up the process of Newton's Method. Next, we talked about TI 89 calculators. They are amazing and can do it all, so if you want to borrow one, just talk to Mr. O'Brien, cause he has a bunch of extra and unused ones.
Next we moved on to Unit 3, which is all about the physical application of derivatives, and involves a lot of word problems.
We started with an example about a square: you have a square and the sides increase at a rate of 2cm/sec. When it has sides of 4X4, what is the rate of change of the area?.. Solve with no calculus, just middle school math.
We said that x (the side length) has a constant rate of change, but the change in area was not. We compared the square when it was a 4X4 at t=2 (the starting value for time) and when it was 6X6 at t=3 seconds. We said that the rate of change over the interval
was the 
or 
which equals 20. But this wasn't the rate of change at exactly the time when the box is a 4X4, so we did the same thing with smaller and smaller intervals. We did t=2 and t=2.1, and t=2 and t=2.01. Then Ann suggested we used the idea from the symmetric difference quotient in this situation. So we did the changes in the rates for t=2.01 and t=1.99, and found the rate of change to be 16 cm2/sec. This is the instantaneous rate of change at the moment in time when the square is a 4X4. We know from calculus that this instantaneous ROC is the limit, and that we can find the ROC using calculus and it would be a lot less work.
This brought us into the idea of Related Rates. These are problems where there are variables that change with varying time. To understand this better we looked at the example of
as well as a #14 and #18 on page 206.
For the problem of a we said that 
= 2 cm/sec and we were trying to find 
. (where x is the side length, t is time, and A is area)
The first step is to take the derivative, remembering that you have to use implicit differentiation and the chain rule, and that there is always a derivative for varying parts.
When x is 4,
We then moved onto the book problems, and Mr. O'Brien said that know formulas (like for volume and area) are important, and that if we forget them we can just google it.
#4 on p. 206 asked about a cone, with radius r and height h. We used the equation for the volume of a cone:
. Part a asked how the derivative of Volume with respect to time is related to the derivative of height with respect to time if r is constant. To do this, we first took the derivative:
1. We said that
was a constant (since r was a constant for this question) and therefore when we took the derivative it looked like this:
. It is very important to remember the chain rule with these problems. Therefore the answer to the problem was that dV/dt is directly proportional to dh/dt if r is constant.
We then did part b, where h is constant, which was largely the same process, just with different variables.
Part c said r and h were both variable. In this case, it was necessary to use the product rule. We still said that the 1/3Ï€ was a constant, so we took it out as we found the derivative of h and
using the product rule (without forgetting to use the chain rule when necessary). What we found was that there was a complicated relationship that looked like this:
.
We then did another example, #18 on p. 206 which was a word problem about water flowing from a conical pile. When doing these kinds of word problems, there are some steps that make it a little easier.
1. Read the problem carefully
2. Make a picture
3. Identify what the variables are and the different rates
4. Find which equations you're going to need
5. If you can, combine variables by subbing in and using pre calculus math
There is homework with more of these problems, and Mr. O'Brien said that's its important to look at them all so that we can get used to solving them, and there's a supercorrections test on wednesday.
Here's a good site that gives some steps for solving related rates questions and has some animations. http://astro.ocis.temple.edu/~dhill001/relatedrates/relatedrates.html
UPDATE
The most important part of solving related rates problems is to clearly understand the problem before beginning it, so all the variables and constants are related correctly. This site: http://tutorial.math.lamar.edu/Classes/CalcI/RelatedRates.aspx has a lot of good examples and explanations. This video: http://www.youtube.com/watch?v=Zdc6Ih-ROt8 shows a related rates problem with trigonometry, and he makes it pretty easy to understand despite a little cold. Another important thing to remember about related rates is that they use implicit differentiation, so it's important to remember which variables go where and to remember all the dx and dy's.
Next we moved on to Unit 3, which is all about the physical application of derivatives, and involves a lot of word problems.
We started with an example about a square: you have a square and the sides increase at a rate of 2cm/sec. When it has sides of 4X4, what is the rate of change of the area?.. Solve with no calculus, just middle school math.
We said that x (the side length) has a constant rate of change, but the change in area was not. We compared the square when it was a 4X4 at t=2 (the starting value for time) and when it was 6X6 at t=3 seconds. We said that the rate of change over the interval
This brought us into the idea of Related Rates. These are problems where there are variables that change with varying time. To understand this better we looked at the example of
For the problem of a
The first step is to take the derivative, remembering that you have to use implicit differentiation and the chain rule, and that there is always a derivative for varying parts.
When x is 4,
We then moved onto the book problems, and Mr. O'Brien said that know formulas (like for volume and area) are important, and that if we forget them we can just google it.
#4 on p. 206 asked about a cone, with radius r and height h. We used the equation for the volume of a cone:
1. We said that
We then did part b, where h is constant, which was largely the same process, just with different variables.
Part c said r and h were both variable. In this case, it was necessary to use the product rule. We still said that the 1/3Ï€ was a constant, so we took it out as we found the derivative of h and
We then did another example, #18 on p. 206 which was a word problem about water flowing from a conical pile. When doing these kinds of word problems, there are some steps that make it a little easier.
1. Read the problem carefully
2. Make a picture
3. Identify what the variables are and the different rates
4. Find which equations you're going to need
5. If you can, combine variables by subbing in and using pre calculus math
There is homework with more of these problems, and Mr. O'Brien said that's its important to look at them all so that we can get used to solving them, and there's a supercorrections test on wednesday.
Here's a good site that gives some steps for solving related rates questions and has some animations. http://astro.ocis.temple.edu/~dhill001/relatedrates/relatedrates.html
UPDATE
The most important part of solving related rates problems is to clearly understand the problem before beginning it, so all the variables and constants are related correctly. This site: http://tutorial.math.lamar.edu/Classes/CalcI/RelatedRates.aspx has a lot of good examples and explanations. This video: http://www.youtube.com/watch?v=Zdc6Ih-ROt8 shows a related rates problem with trigonometry, and he makes it pretty easy to understand despite a little cold. Another important thing to remember about related rates is that they use implicit differentiation, so it's important to remember which variables go where and to remember all the dx and dy's.
Saturday, November 13, 2010
Friday, November 12, 2010
Tuesday, November 2, 2010
Tuesday, November 2 - Review for the test and memorized values
Scribe post can be found here.
Also, if you're a Quizlet kind of person, I've made a Quizlet of all the memorized values, plus a couple of extras.
Friday, October 29, 2010
Friday, October 29 - FINISHING DERIVATIVES!
We're a quarter of the way there, everyone!
Class was 10 minute shorter today because CHills loves its football team. First we talked about the last quiz. It didn't go so well... so Mr O'B said that if anyone decides not to count this quiz grade, that would be okay with him.
The solutions are online, but here are the specific things we went over on the quiz:
#1. Set the equation up like (tan(4x/5))^3 and then proceed.
#3a. Use either calculus or the quadratic equation to find the x- and y-coordinates of the maximum point. Putting those 2 coordinates into (f)' gives you the slope. Put it all together and what do you got? Bippity, boppity, normal line.
b. Here you are looking for two vertical lines - you don't need point-slope. Set your derivative equal to zero and solve.
#4. Use implicit differentiation to solve. Remember when you take the derivative of a y term, you need to take the derivative of that y part and then multiply by y'.
#5. The velocity curve changes direction when the slope goes from negative to positive. To draw the speed curve, just change all the negative values to positive values.
#6. It was agreed by all present that this one was a toughie. Use the Quotient Rule - pay attention to order! And remember this trick - when you take out the greatest common factor, that will help you cancel and simplify. There may be one like this on our next Opportunity Day...?
#7. Ch-ch-ch-chain rule. The derivative of e raised to a power is itself. Then you need to multiply that derivative by the derivative of the power. This one is similar to 27-57 on Assignment #9.
#8. Use Product Rule and treat x and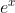
as separate functions.
Whew.
Words of wisdom from O'B: be economic with your space, keep your work clear, and (DEFINITELY)^3 figure out what you did wrong on quizzes after you get them back.
We talked about how d/dx [y] means the same thing as dy/dx - the derivative of the function y. (We quickly went over derivative notation in relation to slope. If you still don't understand, check out http://www4.ncsu.edu/unity/lockers/users/f/felder/public/kenny/papers/dx.html to get a clearer idea of this. But Mr. O'B said not to stress it too much.)
Then we said goodbye to Collin and talked about Part II of the exploration. The solutions for this are online.
In #2, we transformed y=lnx into y' by using implicit differentiation. So, this is a new derivative to know:
.
Question: should we memorize this or just be able to derive it from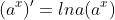
?
Answer: Memorize it.
Check out this graph for a visual connection to the derivative of the natural log function.
#4 talks about the derivative of an inverse function, which is going to be (1/the derivative of its inverse). In other words,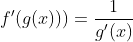
. We found this relationship by differentiating with the chain rule idea that f(g(x)=x.
Then we opened up Geogebra to look at inverse functions. We graphed
. Dan chose an x-value, 3, and we used the function to find the point (3,6) - in blue on my graph. Next, we found the inverse function by using basic log rules: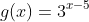 
. We added the inverse point (6, 3) - in black on my graph.
Note: the x and y scales on these axes are not equal.
Then we tried to find an equation of the tangent to f(x) at the "Dan Point" and an equation of the tangent for g(x) at the "Inverse Dan Point". You can do this using your TI by can find the slope with nDeriv - but in the graph window you can do Calc and option 6: dy/dx!
We found both our tangents at the Dan Point (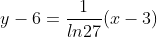
) and the tangent at the Inverse Dan Point.
Here's the previous graph with the tangents added:
In this graph, the red line is the derivative to f(x) at Dan's Point, A. The purple line is the derivative to g(x), the inverse of f(x), at Inverse Dan Point, B. The dotted line is at y=x to show that f(x) and g(x) really are inverses.
Finally, we used Wolframalpha to find the derivatives to the Inverse Trig functions:
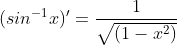
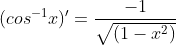
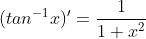
We quickly went over what an inverse trig function means - you are using a trig value to find the angle that has that value. For example,
is asking you to find the values of x for which cos(x) = 1.
If you'd like to see some proofs of the inverse trig derivatives, check out this helpful site. Just click on the one you want and it will take you to that proof: http://www.themathpage.com/aCalc/inverse-trig.htm#arcsin.
Keep up with homework. We have three days of review before the Unit 2 TEST! Happy Halloween everyone!
BLOG POST UPDATE:
Here is a simple diagram to help demonstrate how a trig function and its inverse are related:
For a step-by-step proof of the derivative of the inverse sine function, check this out:
Begin: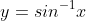
Take the sin of both sides: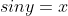
Take the derivative of both sides: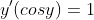
Simplify: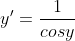
But since we want this derivative to be in terms of x and not in terms of y, let's use the Pythagorean trig identity to simplify.
Pythagorean Identity: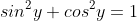
Sub in for y using earlier equation: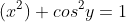
Solve for cosy: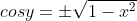
Since we're taking cosine of an inverse sine (which would be in the first or fourth quadrant), we know we need the positive value. So...
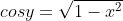
Then sub this back into the equation we found for y':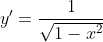
So,
!
To find the derivative of inverse cosine, you would follow the same process but use different substitutions. Remember to pay attention to negative signs.
That's all for now folks.
Class was 10 minute shorter today because CHills loves its football team. First we talked about the last quiz. It didn't go so well... so Mr O'B said that if anyone decides not to count this quiz grade, that would be okay with him.
The solutions are online, but here are the specific things we went over on the quiz:
#1. Set the equation up like (tan(4x/5))^3 and then proceed.
#3a. Use either calculus or the quadratic equation to find the x- and y-coordinates of the maximum point. Putting those 2 coordinates into (f)' gives you the slope. Put it all together and what do you got? Bippity, boppity, normal line.
b. Here you are looking for two vertical lines - you don't need point-slope. Set your derivative equal to zero and solve.
#4. Use implicit differentiation to solve. Remember when you take the derivative of a y term, you need to take the derivative of that y part and then multiply by y'.
#5. The velocity curve changes direction when the slope goes from negative to positive. To draw the speed curve, just change all the negative values to positive values.
#6. It was agreed by all present that this one was a toughie. Use the Quotient Rule - pay attention to order! And remember this trick - when you take out the greatest common factor, that will help you cancel and simplify. There may be one like this on our next Opportunity Day...?
#7. Ch-ch-ch-chain rule. The derivative of e raised to a power is itself. Then you need to multiply that derivative by the derivative of the power. This one is similar to 27-57 on Assignment #9.
#8. Use Product Rule and treat x and
Whew.
Words of wisdom from O'B: be economic with your space, keep your work clear, and (DEFINITELY)^3 figure out what you did wrong on quizzes after you get them back.
We talked about how d/dx [y] means the same thing as dy/dx - the derivative of the function y. (We quickly went over derivative notation in relation to slope. If you still don't understand, check out http://www4.ncsu.edu/unity/lockers/users/f/felder/public/kenny/papers/dx.html to get a clearer idea of this. But Mr. O'B said not to stress it too much.)
Then we said goodbye to Collin and talked about Part II of the exploration. The solutions for this are online.
In #2, we transformed y=lnx into y' by using implicit differentiation. So, this is a new derivative to know:
Question: should we memorize this or just be able to derive it from
Answer: Memorize it.
Check out this graph for a visual connection to the derivative of the natural log function.
#4 talks about the derivative of an inverse function, which is going to be (1/the derivative of its inverse). In other words,
Then we opened up Geogebra to look at inverse functions. We graphed
Note: the x and y scales on these axes are not equal.Then we tried to find an equation of the tangent to f(x) at the "Dan Point" and an equation of the tangent for g(x) at the "Inverse Dan Point". You can do this using your TI by can find the slope with nDeriv - but in the graph window you can do Calc and option 6: dy/dx!
We found both our tangents at the Dan Point (
Here's the previous graph with the tangents added:
In this graph, the red line is the derivative to f(x) at Dan's Point, A. The purple line is the derivative to g(x), the inverse of f(x), at Inverse Dan Point, B. The dotted line is at y=x to show that f(x) and g(x) really are inverses.
Finally, we used Wolframalpha to find the derivatives to the Inverse Trig functions:
We quickly went over what an inverse trig function means - you are using a trig value to find the angle that has that value. For example,
If you'd like to see some proofs of the inverse trig derivatives, check out this helpful site. Just click on the one you want and it will take you to that proof: http://www.themathpage.com/aCalc/inverse-trig.htm#arcsin.
Keep up with homework. We have three days of review before the Unit 2 TEST! Happy Halloween everyone!
BLOG POST UPDATE:
Here is a simple diagram to help demonstrate how a trig function and its inverse are related:
For a step-by-step proof of the derivative of the inverse sine function, check this out:Begin:
Take the sin of both sides:
Take the derivative of both sides:
Simplify:
But since we want this derivative to be in terms of x and not in terms of y, let's use the Pythagorean trig identity to simplify.
Pythagorean Identity:
Sub in for y using earlier equation:
Solve for cosy:
Since we're taking cosine of an inverse sine (which would be in the first or fourth quadrant), we know we need the positive value. So...
Then sub this back into the equation we found for y':
So,
To find the derivative of inverse cosine, you would follow the same process but use different substitutions. Remember to pay attention to negative signs.
That's all for now folks.
Sunday, October 24, 2010
Links for Monday-Wednesday
Exploration
Geogebra File
Solutions to Part 1 of Exploration (to be posted Tuesday)
Solutions to Part 2 of Exploration (to be posted Thursday)
Geogebra File
Solutions to Part 1 of Exploration (to be posted Tuesday)
Solutions to Part 2 of Exploration (to be posted Thursday)
Friday, October 22, 2010
Wednesday, October 20, 2010
Four years free college at USM
Interested in 4 years of college and a laptop for free? This is a pretty cool opportunity:
USM Pioneers
USM Pioneers
Sunday, October 17, 2010
Friday, October 15, 2010
Thursday, October 14, 2010
Scribe Post for Wednesday October 13th
Today in class we started by looking over our unit quiz again. Mr. O'Brien showed us that nDeriv could be used to solve many of the problems like 1 and 2 if we had time to put the correct formatting into our calculator. Just remember that if you want the derivative at a single point the formatting is for example (Y1,X,10) but if you want to find the derivative at all the points if you wanted to graph it the formatting would be (Y1, X, X) to find the values at all points X. Remember that problems like #7 , the only places that the function is not differentiable is at places that there are vertical tangents, cusps, or places that the functions is not defined.
We then talked about the chain rule.
Mathematical
[f(g(x))]' = f '(g(x)) * g '(x)
Verbal
"The derivative of a composition of functions is the derivative of the outer function evaluated at the inner function times the derivative of the inner function."
Lets look at an example
Ex.
The answer to this is
because the outer function is sine,
the inner function is
the derivative of outer = cosine and the derivative of inner = 2x so it’s
derivative of outer evaluated at inner times derivative of inner
cosx2*2x
For more help with the chain rule http://archives.math.utk.edu/visual.calculus/2/chain_rule.4/index.html
The rest of the class we worked on our homework
The quiz on Friday will have chain rule problems on it
Mr. O’Brien says that you have to have the two forms of the derivative memorized the product, quotient, and the chain rule memorized as well as the 6 trig derivatives. 
We then talked about the chain rule.
Mathematical
[f(g(x))]' = f '(g(x)) * g '(x)
Verbal
"The derivative of a composition of functions is the derivative of the outer function evaluated at the inner function times the derivative of the inner function."
Lets look at an example
Ex.
The answer to this is
the inner function is
the derivative of outer = cosine and the derivative of inner = 2x so it’s
derivative of outer evaluated at inner times derivative of inner
cosx2*2x
For more help with the chain rule http://archives.math.utk.edu/visual.calculus/2/chain_rule.4/index.html
The rest of the class we worked on our homework
The quiz on Friday will have chain rule problems on it
Mr. O’Brien says that you have to have the two forms of the derivative memorized the product, quotient, and the chain rule memorized as well as the 6 trig derivatives.
Subscribe to:
Comments (Atom)