QUIZ
BLOG POST
Monday, May 30, 2011
Wednesday, May 18, 2011
Integration by Parts
Integration by parts is a method of solving complicated integrals when the integrand is too tough to be solved with substitution or the reverse chain rule. Integration by parts can be expressed with the following equation:
g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx "\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx")
This equation originates from the product rule. We can find the integration by parts formula by writing out the product rule:
g(x)]=f'(x)g(x) + g'(x)f(x) "\frac{d}{dx}[f(x)g(x)]=f'(x)g(x) + g'(x)f(x)")
When you integrate both sides of the equation, you are left with:
g(x)]=\int f'(x)g(x)dx + \int g'(x)f(x)dx "[f(x)g(x)]=\int f'(x)g(x)dx + \int g'(x)f(x)dx")
Rearranging the terms by subtracting gives you the integration by parts formula that we showed above:
Now that we know where it comes from, we can use integration by parts to solve tricky integration problems. Here's the trickier example that we used in class:
Using substitution doesn't help here, because neither function is really a form of an antiderivative of the other - and trying to do a reverse chain rule with a combination of product rule would probably give you a headache. So, let's use integration by parts.
1. Decide which function in the integrand will be f(x) and which will be g'(x). g'(x) should be one that's easy to antiderive. In this case, let's make
represent g'(x) and 
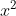represent f(x). This means that f'(x)=2x and g(x)=
.
2. Then, use the integration by parts formula to solve for
= 
- 
Next, simplify.
We'll have to use the integration by parts rule again to solve the last part. Now, f(x)=x but g'(x) is the same as before. When we do that, our equation looks like this:
] "\int x^2e^{2x}= \frac{x^2e^{2x}}{2} - [\frac{xe^{2x}}{2}-\int 1(\frac{e^{2x}}{2})]")
Now, we can simplify and integrate to find our answer... and don't forget the +C!
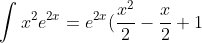 + C "\int x^2e^{2x}= e^{2x}(\frac{x^2}{2}-\frac{x}{2}+1) + C")
It's not pretty, but it's an answer!
Our other example was much simpler -
.
For this one we said that "x=f(x)")
and  "cosx=g'(x)")
.
We then plug into the formula to get this equation:
This simplifies to
and gives you an answer of 
Mr. Khan has a great video to explain integration by parts using a verrrrrry similar example. You can see it by clicking this link:
http://www.khanacademy.org/video/integration-by-parts--part-6-of-indefinite-integration?playlist=Calculus
In our presentation, we broke into groups and used these example problems to help everyone understand the concept of integration by parts. The problems can be found here: http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/intbypartsdirectory/IntByParts.html For each problem, a detailed answer key is given (look to the right of the problem).
We finished our presentation by giving a short quiz.
This equation originates from the product rule. We can find the integration by parts formula by writing out the product rule:
When you integrate both sides of the equation, you are left with:
Rearranging the terms by subtracting gives you the integration by parts formula that we showed above:
Now that we know where it comes from, we can use integration by parts to solve tricky integration problems. Here's the trickier example that we used in class:
Using substitution doesn't help here, because neither function is really a form of an antiderivative of the other - and trying to do a reverse chain rule with a combination of product rule would probably give you a headache. So, let's use integration by parts.
1. Decide which function in the integrand will be f(x) and which will be g'(x). g'(x) should be one that's easy to antiderive. In this case, let's make
2. Then, use the integration by parts formula to solve for
Next, simplify.
We'll have to use the integration by parts rule again to solve the last part. Now, f(x)=x but g'(x) is the same as before. When we do that, our equation looks like this:
Now, we can simplify and integrate to find our answer... and don't forget the +C!
It's not pretty, but it's an answer!
Our other example was much simpler -
For this one we said that
We then plug into the formula to get this equation:
This simplifies to
Mr. Khan has a great video to explain integration by parts using a verrrrrry similar example. You can see it by clicking this link:
http://www.khanacademy.org/video/integration-by-parts--part-6-of-indefinite-integration?playlist=Calculus
In our presentation, we broke into groups and used these example problems to help everyone understand the concept of integration by parts. The problems can be found here: http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/intbypartsdirectory/IntByParts.html For each problem, a detailed answer key is given (look to the right of the problem).
We finished our presentation by giving a short quiz.
Wednesday, May 11, 2011
Student Feedback
Your honest feedback is appreciated:
http://www.surveygizmo.com/s3/536408/Student-Feedback-for-Mr-O-Brien-2011
http://www.surveygizmo.com/s3/536408/Student-Feedback-for-Mr-O-Brien-2011
Thursday, May 5, 2011
Subscribe to:
Comments (Atom)