Our shared revision guide
Answer form for 1998 Section I Part A (55 minutes, 28 questions, non-calculator, beginning on p. 125)
Thursday, March 31, 2011
Wednesday, March 30, 2011
Wednesday, March 23, 2011
Monday, March 21, 2011
Scribe Post 3/21/11
We started off today with a little untimed trig quiz.
Then we moved on to a practice FRQ, #1 from 2008B.
This problem deals with area between two curves, and the volume of that section when it's rotated around the y-axis.
The graph would look like this:

a.)For this part we did an integral from 0 to 9, since the graphs intersect at (9,3).
-\frac{x}{3} \displaystyle \right )dx)
It's also possible to take horizontal slices of the graph and do right minus left and do the integral in terms on y. Like this:

This gives you an answer of 4.5. On this question you got a point for the limits, the integrand, and the answer. Remember that it is important to write down just what you want the reader to see when they're grading your FRQ.
b.)This question asked for the volume of the cross section R rotated around x=-1 (see the graph).
We were reminded that when you write something with pi, be careful to not put a rounded decimal before the pi, even if there are three decimal places. For example, do 1/3 pi instead of .333 pi.
To set up the integral, we needed to use dy, so we would be perpendicular to the axis of rotation. It looks kind of like an upside down volcano with a hole in the middle. This makes the disc look like a donut/washer with a thickness of dy.
To get the volume of one of the donuts, we first needed to find the R and the r (which is actually and
and  . The integral looked like this:
. The integral looked like this:
^2-\pi(y^2+1)^2dy)
We got the 3y+1 by doing right - left. For the second radius, we thought of it in the same way. The right point was changing,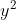 , - the left point of -1. The answer is
, - the left point of -1. The answer is  . You got a point for having the right constants and limits, two points for having the integrand, and one point for the final answer.
. You got a point for having the right constants and limits, two points for having the integrand, and one point for the final answer.
c.) Part c asked for the volume of a solid where the base is region R. For this solid the cross sections perpendicular to the y-axis are squares. The squares are 3D and would come straight out of the board. It's pretty tricky to visualize. It looks kind of like a caterpillar.
First we need to figure out what we are summing for, for our integral. We determined the limits were 0 to 3, and the whole integral was in terms of dy (since it has to be perpendicular to the y-axis). The area of the squares is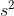 . To find the s we had to right minus left. The integral looks like this:
. To find the s we had to right minus left. The integral looks like this:
^2dy) = 8.1. For this problem you got a point for the integrand, and a point for the limits and the answer.
= 8.1. For this problem you got a point for the integrand, and a point for the limits and the answer.
This problem would be easy if you really understand summing.
Another example is one from the homework. If you have a region bound by two functions, and you are using triangles to sum, you have to find the area of a cross section and multiply by the thickness to find the volume. You are using sums of the area of equilateral triangles. This means you have to find the area of one of the triangles to use in the integral. We looked at an equilateral triangle with a base S, and using area = 1/2 base times height, the area equals\left ( \frac{s}{2} \sqrt(3) \right )) . We used a 30-60-90 triangle to help with this part. The area then equals
. We used a 30-60-90 triangle to help with this part. The area then equals  . The next step is to do the integral. Since we have to do the area of the cross section times the thickness, we use the
. The next step is to do the integral. Since we have to do the area of the cross section times the thickness, we use the  and plug in
and plug in 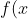-g(x)) for x. This makes the integral
for x. This makes the integral -g(x) \right )^2dx) .
.
Since these can be hard to visualize, there are some links you can use next year when you could possibly be able to use them when you go back to this years blog.
Hooray! We're done! Cross sectional summing is the last thing we're covering this year.
Later this week, we have a test on Friday, all the assignments are due Friday, and Friday is the deadline for all 3rd quarter work.
Links:
http://mathdemos.gcsu.edu/mathdemos/sectionmethod/sectionmethod.html
For this one, you have to click the big square button, but it shows what the shape looks like.
http://www.slu.edu/classes/maymk/banchoff/SolidsOfIntegration.html
Then we moved on to a practice FRQ, #1 from 2008B.
This problem deals with area between two curves, and the volume of that section when it's rotated around the y-axis.
The graph would look like this:

a.)For this part we did an integral from 0 to 9, since the graphs intersect at (9,3).
It's also possible to take horizontal slices of the graph and do right minus left and do the integral in terms on y. Like this:
This gives you an answer of 4.5. On this question you got a point for the limits, the integrand, and the answer. Remember that it is important to write down just what you want the reader to see when they're grading your FRQ.
b.)This question asked for the volume of the cross section R rotated around x=-1 (see the graph).
We were reminded that when you write something with pi, be careful to not put a rounded decimal before the pi, even if there are three decimal places. For example, do 1/3 pi instead of .333 pi.
To set up the integral, we needed to use dy, so we would be perpendicular to the axis of rotation. It looks kind of like an upside down volcano with a hole in the middle. This makes the disc look like a donut/washer with a thickness of dy.
To get the volume of one of the donuts, we first needed to find the R and the r (which is actually
We got the 3y+1 by doing right - left. For the second radius, we thought of it in the same way. The right point was changing,
c.) Part c asked for the volume of a solid where the base is region R. For this solid the cross sections perpendicular to the y-axis are squares. The squares are 3D and would come straight out of the board. It's pretty tricky to visualize. It looks kind of like a caterpillar.
First we need to figure out what we are summing for, for our integral. We determined the limits were 0 to 3, and the whole integral was in terms of dy (since it has to be perpendicular to the y-axis). The area of the squares is
This problem would be easy if you really understand summing.
Another example is one from the homework. If you have a region bound by two functions, and you are using triangles to sum, you have to find the area of a cross section and multiply by the thickness to find the volume. You are using sums of the area of equilateral triangles. This means you have to find the area of one of the triangles to use in the integral. We looked at an equilateral triangle with a base S, and using area = 1/2 base times height, the area equals
Since these can be hard to visualize, there are some links you can use next year when you could possibly be able to use them when you go back to this years blog.
Hooray! We're done! Cross sectional summing is the last thing we're covering this year.
Later this week, we have a test on Friday, all the assignments are due Friday, and Friday is the deadline for all 3rd quarter work.
Links:
http://mathdemos.gcsu.edu/mathdemos/sectionmethod/sectionmethod.html
For this one, you have to click the big square button, but it shows what the shape looks like.
http://www.slu.edu/classes/maymk/banchoff/SolidsOfIntegration.html
Friday, March 18, 2011
Assignment #7 Even Answers
46.
a. π[3 – ln4]
b. 17π/3
c. π[ln(4)-1]
52.
V = 36π/5, so W = 8.5 * 36π/5 = 192 g
a. π[3 – ln4]
b. 17π/3
c. π[ln(4)-1]
52.
V = 36π/5, so W = 8.5 * 36π/5 = 192 g
Wednesday, March 16, 2011
Extra Credit Opportunity!
Watch this video:
http://vihart.com/blog/pi-is-still-wrong/
Check out the Tau Manifesto:
http://tauday.com/
Share your thoughts in the comments...
http://vihart.com/blog/pi-is-still-wrong/
Check out the Tau Manifesto:
http://tauday.com/
Share your thoughts in the comments...
Monday, March 14, 2011
Thursday, March 10, 2011
Trig, Khan Academy, and class
1. Take this 2 minute practice trig quiz (15 questions...).
2. Take the class quiz.
3. Please register for the Khan Academy. Use my email address under the Add a Coach link.
4. Let's do some practice...
5. Please watch this video before next class.
Wednesday, March 9, 2011
Tuesday, March 8, 2011
Monday, March 7, 2011
Thursday, March 3, 2011
Integrals by Substitution 3/3/11
Scribe Post for March 3, 2011
Subscribe to:
Comments (Atom)
